A and B entered into a partnership investing Rs 16000 and Rs. 12000 respectively. After 3 months A withdrew Rs. 5000 while B invested Rs. 5000 more. After 3 more months C joins the business with a capital of Rs 21000. The share of B exceeds that of C, out of a total profit of Rs. 26400 after one year by

Correct Answer Is : Rs. 3600

Solution Is : Ratio of equivalent capitals of A,B and C for 1 month = (16000 * 3 + 11000 * 9) : ( 12000 *3 + 17000 *9): (21000 *6) = (48000 + 99000) : ( 36000 + 153000) : 126000 = 147000:189000 :126000 = 49: 63 : 42 = 7: 9 : 6 . Sum of ratios +7+9+6 =22. Therefore required difference =Rs.((9-6)/22) * 26400) = Rs. (3* 26400)/22 =Rs.3600.

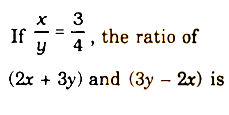
Correct Answer Is : 3:1

Solution Is :

What must be added to each term of the ratio 2:5 so that it may equal to 5:6?

Correct Answer Is : 13

Solution Is : According to question (2+x)/(5+x) = 5/6
⇒ 12+6x = 25+5x ⇒x=25-12 =13

If 3/4 of a number is 7 more then 1/6 of the number, then 5/3 of the number is

Correct Answer Is : 20

Solution Is : Let the number be x.
⇒ (3/4)x=(1/6)x+7
⇒ (3/4)x-(1/6)x =7
⇒ (9x-2x)/12 =7
⇒(7/12)x =7 . Therefore x=12.
Now 5/3 of x =(5/3)*12 =20

If A and B are in the ratio 4:5 and the difference of their squares is 81, what is the value of A?

Correct Answer Is : 12

Solution Is :
Ratio Now , B²-A²=81 A/B =4/5
⇒ B/A =5/4.
Squaring both sides , we get
⇒B²/A² =25/16.
Both sides subtract 1
=⇒(B²-A²)/A² =(25-16)/16 =9/16
⇒81/A² =9/16
⇒ A² =16*9 ⇒ A=12

If two numbers are in the ratio 2 : 3 and the ratio becomes 3 : 4 when 8 is added to both the numbers is

Correct Answer Is : 40

Solution Is :

The ratio of the first and second class fares between two stations is 4 : 1 and that of the number of passengers travelling by the first and second class is 1 : 40. If Rs. 11000 is collected as total fare, then the amount collected from the first class passengers is

Correct Answer Is : Rs. 1000

Solution Is : Let number of passengers in first class be x and number of passengers in second class be 40x. Then, total amount of first class =4x and total amount of second class =40x Ratio of the amounts collected from the first class and the second class passengers = 4 : 40 Amount collected from the first class passengers

The ratio of two numbers is 3 : 4 and their LCM is 180. The second number is

Correct Answer Is : 60

Solution Is : Numbers = 3x and 4x
Their LCM = 3*4*x =12x.
Therefore 12x=180 =⇒
x=180/12 =15.
Second number=4x = 4*15=60.

Which of the following represents a correct proportion?

Correct Answer Is : 12:9 = 16:12

Solution Is : (12/9)=(16/12)
⇒12*12=9*16
⇒ 144=144

Three numbers are in the ratio 1 : 2 : 3 and their HCF is 12. The numbers are

Correct Answer Is : 12, 24, 36

Solution Is : we know that the H.C.F. of two or more algebraical expression of highest dimensions which divides each of them without remainder. given numbers are in the ratio 1:2:3 let the nos.are 1*x,2*x,3*x so we can write, x=12 (here `x` is the highest dimension and divides the nos without remainder) So the nos. are, 1*12,2*12,3*12 i.e. 12,24,36