Digitization help student to explore and study their academic courses online, as this gives them flexibility and scheduling their learning at their convenience. Kidsfront has prepared unique course material of SSC CHSL Quantative Aptitude Mensuration for SSC CHSL Exam student. This free online SSC CHSL Quantative Aptitude study material for SSC CHSL Exam will help students in learning and doing practice on Mensuration topic of SSC CHSL Exam SSC CHSL Quantative Aptitude. The study material on Mensuration, help SSC CHSL Exam SSC CHSL Quantative Aptitude students to learn every aspect of Mensuration and prepare themselves for exams by doing online test exercise for Mensuration, as their study progresses in class. Kidsfront provide unique pattern of learning SSC CHSL Quantative Aptitude with free online comprehensive study material and loads of SSC CHSL Exam SSC CHSL Quantative Aptitude Mensuration exercise prepared by the highly professionals team. Students can understand Mensuration concept easily and consolidate their learning by doing practice test on Mensuration regularly till they excel in SSC CHSL Quantative Aptitude Mensuration.
 A metal sphere of radius 5 cm is melted to make a cone with base of the same radius. What is the height of the cone ?
A metal sphere of radius 5 cm is melted to make a cone with base of the same radius. What is the height of the cone ? Correct Answer Is : 20 cm
Correct Answer Is : 20 cm A person standing on the bank of river observes that the angle of elevation of the top of tree standing on the opposite bank is 60
A person standing on the bank of river observes that the angle of elevation of the top of tree standing on the opposite bank is 60 Correct Answer Is : 34.64 m
Correct Answer Is : 34.64 m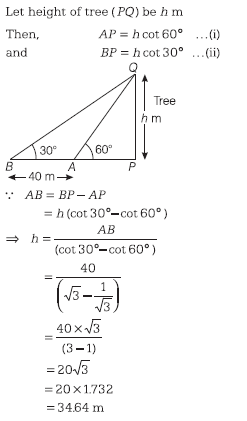
 From the top of a cliff 90 m high, the angles of depression of the top and bottom of a tower are observed to be 30
From the top of a cliff 90 m high, the angles of depression of the top and bottom of a tower are observed to be 30 Correct Answer Is : 60 m
Correct Answer Is : 60 m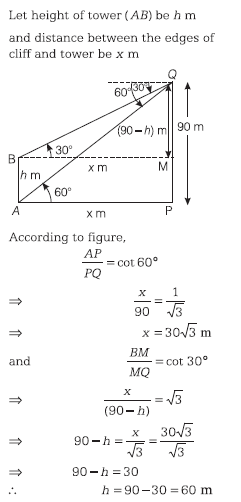
 The area of rectangle is 108 m2 and the ratio of length and width is 3 : 4, then find the value of A0
The area of rectangle is 108 m2 and the ratio of length and width is 3 : 4, then find the value of A0 Correct Answer Is : 7.5 m
Correct Answer Is : 7.5 m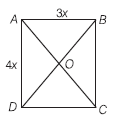
 The least value of (4 sec2θ + 9 cosec2θ) is
The least value of (4 sec2θ + 9 cosec2θ) is Correct Answer Is : 25
Correct Answer Is : 25 The radius of a circle is 13 cm and xy is a chord which is at a distance of 12 cm from the centre. The length of the chord is
The radius of a circle is 13 cm and xy is a chord which is at a distance of 12 cm from the centre. The length of the chord is  Correct Answer Is : 10 cm
Correct Answer Is : 10 cm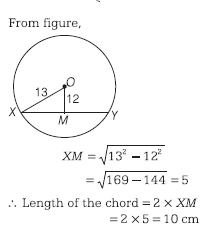
 If three metallic spheres of radii 6 cm, 8 cm and 10 cm are melted to form a single sphere, then the diameter of the new sphere will be
If three metallic spheres of radii 6 cm, 8 cm and 10 cm are melted to form a single sphere, then the diameter of the new sphere will be Correct Answer Is : 24 cm
Correct Answer Is : 24 cm Two circular metallic discs have a thickness of 15 mm. Their areas are in the ratio of 9 : 1. The smaller dia disc is pressed against the bigger disc and rotated around it on a flat surface. How many times will the small disc rotate before it completes one circle of the bigger disc?
Two circular metallic discs have a thickness of 15 mm. Their areas are in the ratio of 9 : 1. The smaller dia disc is pressed against the bigger disc and rotated around it on a flat surface. How many times will the small disc rotate before it completes one circle of the bigger disc? Correct Answer Is : 3
Correct Answer Is : 3 A metallic cuboid weighs kg. How much would a miniature cuboid of metal weigh, if all the dimensions are reduced to 1/4th of the original?
A metallic cuboid weighs kg. How much would a miniature cuboid of metal weigh, if all the dimensions are reduced to 1/4th of the original? Correct Answer Is : 0.25 kg
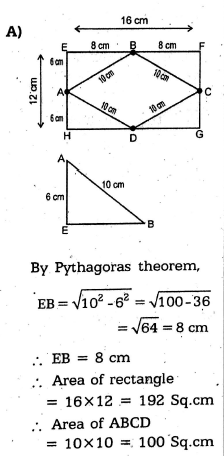
Correct Answer Is : 0.25 kg ABCD are midpoints of the rectangle. AB= 10 cm, If one of the sides of the rectangle is 12 cm, then what is the area of ABCD?
ABCD are midpoints of the rectangle. AB= 10 cm, If one of the sides of the rectangle is 12 cm, then what is the area of ABCD?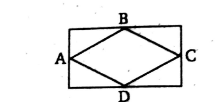
 Correct Answer Is : 100 sq cm
Correct Answer Is : 100 sq cm