Learn Quantitative Aptitude Geometry, SSC SI CAPF Exam Quantitative Aptitude Geometry Exercise, Free Online Geometry Lessons

SSC SI CAPF Exam Quantitative Aptitude Study Material

Digitization help student to explore and study their academic courses online, as this gives them flexibility and scheduling their learning at their convenience. Kidsfront has prepared unique course material of Quantitative Aptitude Geometry for SSC SI CAPF Exam student. This free online Quantitative Aptitude study material for SSC SI CAPF Exam will help students in learning and doing practice on Geometry topic of SSC SI CAPF Exam Quantitative Aptitude. The study material on Geometry, help SSC SI CAPF Exam Quantitative Aptitude students to learn every aspect of Geometry and prepare themselves for exams by doing online test exercise for Geometry, as their study progresses in class. Kidsfront provide unique pattern of learning Quantitative Aptitude with free online comprehensive study material and loads of SSC SI CAPF Exam Quantitative Aptitude Geometry exercise prepared by the highly professionals team. Students can understand Geometry concept easily and consolidate their learning by doing practice test on Geometry regularly till they excel in Quantitative Aptitude Geometry.

Geometry

Internal bisectors of ∠Q and ∠R of ΔPQR intersect at 0. If ∠ROQ = 96° then the value of ∠RPQ is

a) 12°
b) 6°
c) 36°
d) 24°

✔Answer

✔Solution

Correct Answer Is : 12°

Solution Is :

If the sum and difference of two angles are 22/9 radian and 36° respectively, then the value of smaller angle in degree taking the value of π as 22/7 is :

a) 60°
b) 48°
c) 52°
d) 56°

✔Answer

✔Solution

Correct Answer Is : 52°

Solution Is : Let angles are X and Y rad.
X-Y=36° --- (i)
X+Y =22/9
X+Y=(22/9)*(180/π) =440°/π =140°. ----(ii)
Now, on solving (i) and(ii), we get X=68°
and Y=52°. So smaller angle =52°.

If θ be acute angle and tan(4θ -50°) = cot(50°-θ), then the value of θ in degrees is

a) 30
b) 40
c) 20
d) 50

✔Answer

✔Solution

Correct Answer Is : 30

Solution Is : Tan(4θ- 50°) = cot(50°-θ )
⇒tan(4θ- 50°) = tan(90 - (50° -θ))
⇒ 4θ- 50° = 90 -50°+θ
⇒ 3θ= 90°
θ = 30°.

Given that : ΔABC ΔPQR, If area(?PQR)/area(?ABC) = 256/441 and PR=12 cm, then AC is equal to

a) 15.75 cm
b) 16 cm
c) 12 cm
d) 15.5 cm

✔Answer

✔Solution

Correct Answer Is : 15.75 cm

Solution Is : The ratio of the areas of two similar triangles is equal to the ratio of squares of any two corresponding sides.
Therefore, (Area of Δ PQR)/(Area of Δ ABC)=(PR ²)/AC² (PR ²)/AC² = 256/441 (12 ²)/AC² = 256/441
Taking square roots of both sides,
12/AC=16/21
⇒16×AC=12×21
⇒ AC = (12×21)/16=63/4
=15.75 cm

In ΔABC, D and E are two mid points of sides AB and AC respectively. If ∠BAC = 40° and ∠ABC = 65° then ∠CED is :

a) 130°
b) 75°
c) 125°
d) 105°

✔Answer

✔Solution

Correct Answer Is : 105°

Solution Is :

ABCD is a cyclic quadrilateral. Diagonals AC and BD meets at P. If ∠APB = 110° and ∠CBD = 30°, then ∠ADB measures

a) 55°
b) 30°
c) 70°
d) 80°

✔Answer

✔Solution

Correct Answer Is : 80°

Solution Is :

O is the circumcentre of ΔABC. If ∠BAC = 85°, ∠BCA = 75°, then ∠OAC is equal to :

a) 60°
b) 70°
c) 50°
d) 40°

✔Answer

✔Solution

Correct Answer Is : 70°

Solution Is :

O is the in centre of ΔPQR and ΔQPR = 50°, then the measure of ∠QOR is :

a) 125°
b) 100°
c) 130°
d) 115°

✔Answer

✔Solution

Correct Answer Is : 115°

Solution Is :

The internal bisectors of the ∠B and ∠C of the ΔABC, intersect at O. If ∠A =:100°, then the measure of ∠BOC is :

a) 140°
b) 120°
c) 110°
d) 130°

✔Answer

✔Solution

Correct Answer Is : 140°

Solution Is :

If PQRS is a rhombus and ∠SPQ = 50°, then ∠RSQ is

a) 55°
b) 65°
c) 75°
d) 45°

✔Answer

✔Solution

Correct Answer Is : 65°

Solution Is :

PREVIOUS NEXT

❏Computer Practice +

❏English Practice +

❏General Knowledge Practice +

❏Logical Reasoning Practice +

❏Quantitative Aptitude Practice +

SSC SI CAPF Exam Quantitative Aptitude Study Material

Geometry

Internal bisectors of ∠Q and ∠R of ΔPQR intersect at 0. If ∠ROQ = 96° then the value of ∠RPQ is

Correct Answer Is : 12°

Solution Is :

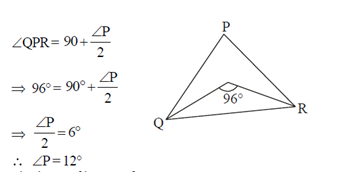
If the sum and difference of two angles are 22/9 radian and 36° respectively, then the value of smaller angle in degree taking the value of π as 22/7 is :

Correct Answer Is : 52°

Solution Is : Let angles are X and Y rad. X-Y=36° --- (i) X+Y =22/9 X+Y=(22/9)*(180/π) =440°/π =140°. ----(ii) Now, on solving (i) and(ii), we get X=68° and Y=52°. So smaller angle =52°.

If θ be acute angle and tan(4θ -50°) = cot(50°-θ), then the value of θ in degrees is

Correct Answer Is : 30

Solution Is : Tan(4θ- 50°) = cot(50°-θ ) ⇒tan(4θ- 50°) = tan(90 - (50° -θ)) ⇒ 4θ- 50° = 90 -50°+θ ⇒ 3θ= 90° θ = 30°.

Given that : ΔABC ΔPQR, If area(?PQR)/area(?ABC) = 256/441 and PR=12 cm, then AC is equal to

Correct Answer Is : 15.75 cm

In ΔABC, D and E are two mid points of sides AB and AC respectively. If ∠BAC = 40° and ∠ABC = 65° then ∠CED is :

Correct Answer Is : 105°

Solution Is :

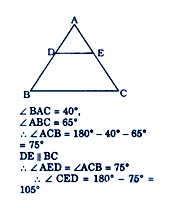
ABCD is a cyclic quadrilateral. Diagonals AC and BD meets at P. If ∠APB = 110° and ∠CBD = 30°, then ∠ADB measures

Correct Answer Is : 80°

Solution Is :

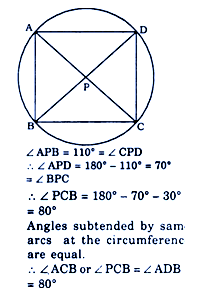
O is the circumcentre of ΔABC. If ∠BAC = 85°, ∠BCA = 75°, then ∠OAC is equal to :

Correct Answer Is : 70°

Solution Is :

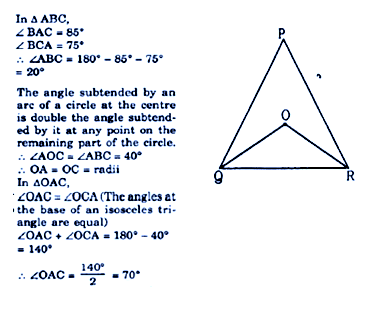
O is the in centre of ΔPQR and ΔQPR = 50°, then the measure of ∠QOR is :

Correct Answer Is : 115°

Solution Is :

The internal bisectors of the ∠B and ∠C of the ΔABC, intersect at O. If ∠A =:100°, then the measure of ∠BOC is :

Correct Answer Is : 140°

Solution Is :

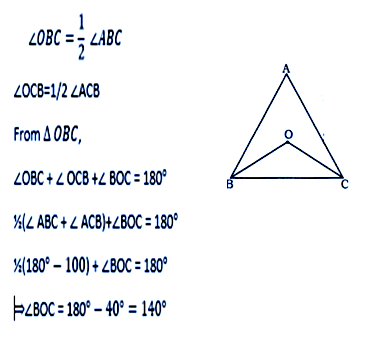
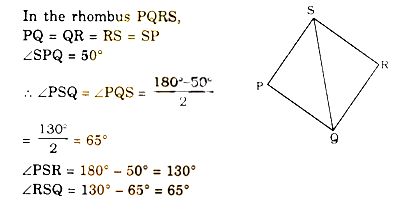
If PQRS is a rhombus and ∠SPQ = 50°, then ∠RSQ is

Correct Answer Is : 65°

Solution Is :

Kids Learning

Academics

Competitive Exams

Govt. Jobs Exams

Solution Is : Let angles are X and Y rad.
X-Y=36° --- (i)
X+Y =22/9
X+Y=(22/9)*(180/π) =440°/π =140°. ----(ii)
Now, on solving (i) and(ii), we get X=68°
and Y=52°. So smaller angle =52°.

Solution Is : Tan(4θ- 50°) = cot(50°-θ )
⇒tan(4θ- 50°) = tan(90 - (50° -θ))
⇒ 4θ- 50° = 90 -50°+θ
⇒ 3θ= 90°
θ = 30°.