Digitization help student to explore and study their academic courses online, as this gives them flexibility and scheduling their learning at their convenience. Kidsfront has prepared unique course material of Quantitative Aptitude Mensuration for IBPS RRB CWE Exam student. This free online Quantitative Aptitude study material for IBPS RRB CWE Exam will help students in learning and doing practice on Mensuration topic of IBPS RRB CWE Exam Quantitative Aptitude. The study material on Mensuration, help IBPS RRB CWE Exam Quantitative Aptitude students to learn every aspect of Mensuration and prepare themselves for exams by doing online test exercise for Mensuration, as their study progresses in class. Kidsfront provide unique pattern of learning Quantitative Aptitude with free online comprehensive study material and loads of IBPS RRB CWE Exam Quantitative Aptitude Mensuration exercise prepared by the highly professionals team. Students can understand Mensuration concept easily and consolidate their learning by doing practice test on Mensuration regularly till they excel in Quantitative Aptitude Mensuration.
The total surface area of a regular triangular pyramid with each edge of length 1 cm is 
Correct Answer Is : √3 cm2 The number of paving stones each measuring 2.5 m x 2m required to pave a rectangular courtyard 30m long and 17.5m wide is Correct Answer Is : 105 The perimeter of a sheet of paper in the shape of a quadrant of a circle is 75 cm. Its area would be ( π = 22/7) Correct Answer Is : 346.5 cm2
The perimeter of two similar triangles are 30 cm and 20 cm respectively. If one side of the first triangles is 9 cm. Determine the corresponding side of the second triangle. Correct Answer Is : 6 cm The diagonal of a quadrilateral shaped field is 24m and the perpendiculars dropped on it from the remaining opposite vertices are 8 cm and 13 cm. The area of the field is Correct Answer Is : 252 m2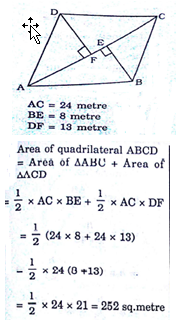
If the base right of right prism remains same and the lateral edges are halved, then its volume will be reduced by Correct Answer Is : 50% The radius of a right circular cone is 3 cm and its height is 4 cm. The total surface area of the cone is Correct Answer Is : 75.4 sq.cm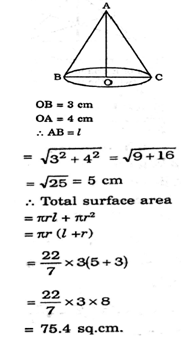
A wooden box of dimensions 8 metre x 7 metre x6 metre is to carry rectangular boxes of dimensions 8 cm x 7 cm x6 cm. The maximum number of boxes that can be carried in 1 wooden box is Correct Answer Is : 1000000 Two circular cylinders of equal volume have their heights in the ratio 1 : 2. Ratio of their radii is Correct Answer Is : √2 : 1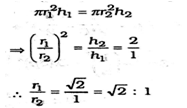
A rectangular piece of paper of dimensions 22 cm by 12 cm is rolled along its length to form a cylinder. The Volume ( in cu. Cm) of the cylinder so formed is Correct Answer Is : 462