Digitization help student to explore and study their academic courses online, as this gives them flexibility and scheduling their learning at their convenience. Kidsfront has prepared unique course material of SSC CHSL Quantative Aptitude Statistics for SSC CHSL Exam student. This free online SSC CHSL Quantative Aptitude study material for SSC CHSL Exam will help students in learning and doing practice on Statistics topic of SSC CHSL Exam SSC CHSL Quantative Aptitude. The study material on Statistics, help SSC CHSL Exam SSC CHSL Quantative Aptitude students to learn every aspect of Statistics and prepare themselves for exams by doing online test exercise for Statistics, as their study progresses in class. Kidsfront provide unique pattern of learning SSC CHSL Quantative Aptitude with free online comprehensive study material and loads of SSC CHSL Exam SSC CHSL Quantative Aptitude Statistics exercise prepared by the highly professionals team. Students can understand Statistics concept easily and consolidate their learning by doing practice test on Statistics regularly till they excel in SSC CHSL Quantative Aptitude Statistics.
 Given the mean of five numbers is 27. If one of them is excluded , the mean gets reduced by 2. Determine the excluded number.
Given the mean of five numbers is 27. If one of them is excluded , the mean gets reduced by 2. Determine the excluded number. Correct Answer Is : 35
Correct Answer Is : 35 If x is the mean of n observations x1 , x2 , ...... xn , then the mean of x1/a , x2/a , ,,,,, xn/a is
If x is the mean of n observations x1 , x2 , ...... xn , then the mean of x1/a , x2/a , ,,,,, xn/a is  Correct Answer Is : X/a
Correct Answer Is : X/a The mean weight of 34 students of a school is 42 kg. If the weight of the teacher be included, the mean rises by 400 g. find the weight of the teacher in kg
The mean weight of 34 students of a school is 42 kg. If the weight of the teacher be included, the mean rises by 400 g. find the weight of the teacher in kg Correct Answer Is : 56
Correct Answer Is : 56 Study the chart and answer the following question
Study the chart and answer the following question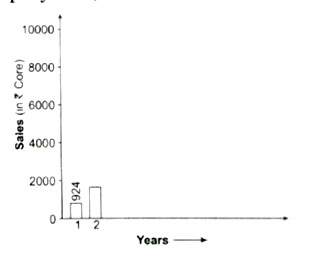
 Correct Answer Is : 4827
Correct Answer Is : 4827 The average marks secured by 36 students was 52. but it was discovered that an item 64 was misred as 64.what is the correct mean of mark?
The average marks secured by 36 students was 52. but it was discovered that an item 64 was misred as 64.what is the correct mean of mark? Correct Answer Is : 52.5
Correct Answer Is : 52.5 The mean high temperature of the first four days of a week is 25°C whereas the mean of the last four days is 25.5°C.
If the mean of the whole week is 25.2°C, then the temperature of the 4th day is
The mean high temperature of the first four days of a week is 25°C whereas the mean of the last four days is 25.5°C.
If the mean of the whole week is 25.2°C, then the temperature of the 4th day is Correct Answer Is : 25.6°C
Correct Answer Is : 25.6°C Find the mean of the first 6 prime numbers?
Find the mean of the first 6 prime numbers?  Correct Answer Is : 41 / 6
Correct Answer Is : 41 / 6 The mean proportion of 1.21 and 0.09 is
The mean proportion of 1.21 and 0.09 is Correct Answer Is : 0.33
Correct Answer Is : 0.33 The arithmetic mean (average) of the first 10 whole numbers is
The arithmetic mean (average) of the first 10 whole numbers is Correct Answer Is : 4.5
Correct Answer Is : 4.5 The mean of 9 observations is 16. One more observation is included and the new mean
becomes 17. The 10th observation is
The mean of 9 observations is 16. One more observation is included and the new mean
becomes 17. The 10th observation is Correct Answer Is : 26
Correct Answer Is : 26