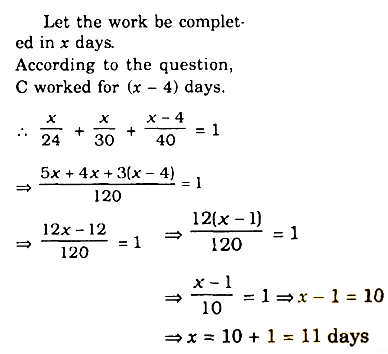Digitization help student to explore and study their academic courses online, as this gives them flexibility and scheduling their learning at their convenience. Kidsfront has prepared unique course material of Quantitative Aptitude Time and Work for IBPS PO CWE Exam student. This free online Quantitative Aptitude study material for IBPS PO CWE Exam will help students in learning and doing practice on Time and Work topic of IBPS PO CWE Exam Quantitative Aptitude. The study material on Time and Work, help IBPS PO CWE Exam Quantitative Aptitude students to learn every aspect of Time and Work and prepare themselves for exams by doing online test exercise for Time and Work, as their study progresses in class. Kidsfront provide unique pattern of learning Quantitative Aptitude with free online comprehensive study material and loads of IBPS PO CWE Exam Quantitative Aptitude Time and Work exercise prepared by the highly professionals team. Students can understand Time and Work concept easily and consolidate their learning by doing practice test on Time and Work regularly till they excel in Quantitative Aptitude Time and Work.
50 workers can complete a job in 6 days working 8 hours a day. If 40 workers are employed to complete the job in 20 days then the number of hours they should be working per day is
Correct Answer Is : 3
A man worked 14 hours a day for the first 2 days, 12 hours a day for the neXt 3 days but did not work on the siXth day. Then on the average how much did he work in the first siX days ? Correct Answer Is : 11 hours 40 minutes Mohan engaged a servant on the condition that he would pay him ₹ 200 and a uniform after 10 days. The servant served only for 5 days and got ₹ 20 and a uniform. Find the price of the uniform. Correct Answer Is : ₹ 160
If 5 men or 9 women can do piece of work in 19days; 3 men and 6 women will do the same work in ---- Correct Answer Is : 15days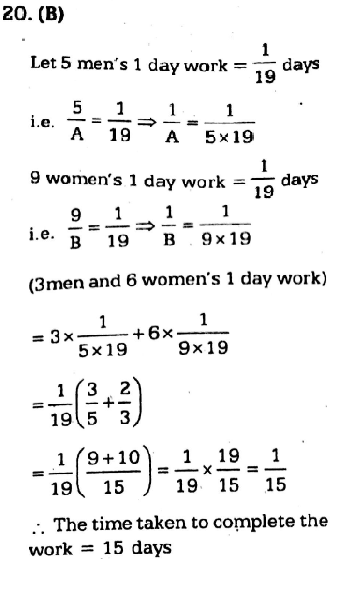
A`s 2 days` work is equal to B`s 3 days` work. If A can complete the work in 8 days then to complete the work B will take Correct Answer Is : 12 days 4 men and 6 women complete a work in 8 days. 2 men and 9 women also complete in 8 days in which. The number of days in which 18 women complete the work is : Correct Answer Is : 5 1/3days If 4 men or 8 women can do a piece of work in 15 days, in how many days can 6 men and 12 women do the same piece of work Correct Answer Is : 15 days If A, B and C can complete a work in 6 days. If A can work twice faster than B and
thrice faster than C, then the number of days C alone can complete the work is : Correct Answer Is : 33 days A and B together can do a .piece of work in 30 days. B and C together can do it in
20 days. A starts the work and works on it for 5 days, then B takes up and works for 15 days. Finally C finishes the work in 18 days. The number of days in which C alone can do the work when doing it separately is : Correct Answer Is : 24 days A, B and C can do a piece of work in 24, 30 and 40 days respectively. They began the work together but C left 4 days before completion of the work. In how many days was the work done ? Correct Answer Is : 11
